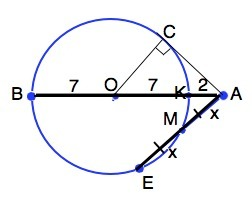
Решение с подробным объяснением.
На рисунке приложения АО - расстояние от точки до центра окружности, ВК - диаметр, АЕ - данная секущая, М - ее середина.
АС - касательная.
По т. о касательной и секущей квадрат отрезка касательной равен произведению секущей, проведенной из той же точки, на ее внешнюю часть. ⇒
АС²=АЕ•АМ
АВ, проходящая через диаметр, - тоже секущая.
АС*=АВ•АК ⇒
АЕ•АМ=АВ•АК
АК=9-7=2 см, АВ+2r+2=16 см
Примем АМ=х
2х•х=16•2 ⇒
х²=16, х=√16=4 см
Секущая АЕ=2х=8 см