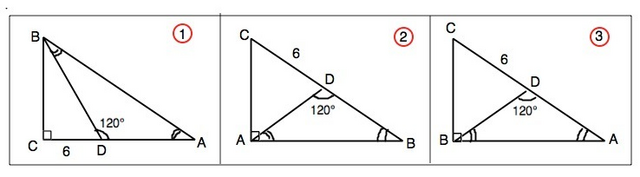
Поскольку прямой угол не указан, задача может иметь два варианта решения.
1)
Угол С=90°
Тогда т.D принадлежит катету АС, так как лежать на АВ не может - не получится угла АDВ=120°
Угол АDВ внешний для ∆ СDВ и равен сумме, не смежных с ним
∠DСВ и ∠DВС (свойство внешнего угла).
В прямоугольном ∆ ВDС угол DВС= 120°-90°=30°
Тогда ВС=DC:tg30•=6√3
∆ АВD - равнобедренный. Его острые углы (180°-120°):2=30°
BC противолежит углу А=30°, поэтому АВ=2•ВС=12√3
2)
Угол А=90°
Тогда в равнобедренном ∆ ВDА острые углы равны 30°. ⇒
угол С=60°
АВ=АС•tg60°=6√3
3)
Угол В=90° Решение аналогично предыдущему и АВ=6√3