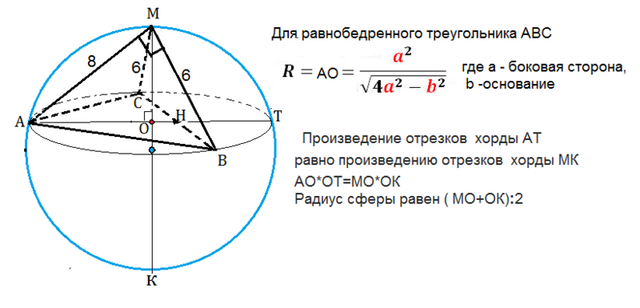
№4 Боковые ребра треугольной пирамиды взаимно перпендикулярны и равны 8, 6, и 6. Найдите радиус описанной около этой пирамиды сферы.
Пусть данная пирамида МАВС. (см. рисунок)
Из условия следует, что боковые грани данной пирамиды - прямоугольные треугольники.
∆ МАС=∆ МВС по равным катетам. ⇒
их гипотенузы равны: АВ=АС.
По т. Пифагора АВ=10.
∆ МСВ - равнобедренный прямоугольный с катетами, равными 6. ⇒
СВ=6√2 .
Пирамида вписанная, все ее точки лежат на поверхности сферы.
Основание пирамиды лежит в плоскости, пересекающей сферу по окружности с радиусом, равным радиусу описанной вокруг АВС окружности. Для радиуса описанной окружности равнобедренного треугольника
R=a² :√(4a² -b² )
R=100:√328=50:√82
Основание высоты МО пирамиды лежит в центре описанной вокруг АВС окружности.
МО из ∆ АОМ по т.Пифагора:
МО =√(АМ² -АО²) =√(64- (50:√82)²)= √2748/82)
Для осевого сечения сферы диаметр АТ сечения и диаметр МК сферы - пересекающиеся хорды.
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. ⇒ АО*ОТ=МО*ОК.
ОК=АО²:МО
ОК=(50:√82)²:√(2748/82)=2500:√225336=5,267
Диаметр сферы МК=МО+ОК=√2748/82)+5,267=5,789+ 5,267= ≈11,056
R =D:2= ≈ 5,528 (ед. длины)