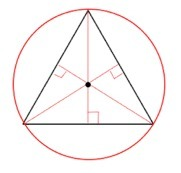
Центр описанной около треугольника окружности лежит в точке пересечения срединных перпендикуляров.
Для равностороннего треугольника это точка пересечения высот,
медиан, биссектрис, т.к. они у него совпадают.
Медианы треугольника пересекаются в отношении 2:1, считая от вершины. Следовательно,
радиус описанной около равностороннего треугольника окружности равен 2/3 его высоты.
R=12:3•2=
8 дм.