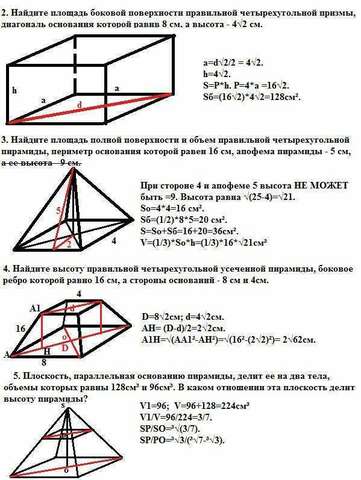
2. Найдите площадь боковой поверхности правильной четырехугольной призмы, диагональ основания которой равна 8 см, а высота - 4√2 см.
Правильная призма — это прямая призма, основанием которой является правильный многоугольник. Боковые грани правильной призмы — равные прямоугольники.
Итак, основание призмы - квадрат, диагональ которого равна 8см.
Мы знаем, что сторона квадрата равна а=d√2/2 (формула).
Площадь боковой поверхности призмы S=P*h, где P — периметр основания призмы, h — высота призмы. В нашем случае а=4√2, значит Р=4*а=16√2, а h=4√2(дано).
Тогда Sб=(16√2)*4√2=128см².
3. Найдите площадь полной поверхности и объем правильной четырехугольной пирамиды, периметр основания которой равен 16 см, апофема пирамиды - 5 см, а ее высота - 9 см. Тут явная ошибка в данных. Если сторона основания равна 16/4=4, апофема = 5, то высота по Пифагору должна быть =√21. (√(25-(4/2)²). Решаем для этих данных:
Мы знаем, что площадь полной поверхности пирамиды равна сумме площади основания (в нашем случае квадрата) и площади боковой поверхности, равной произведению полупериметра на апофему (высоту боковой грани) призмы.
Итак, сторона основания в нашем случае равна 4 см, значит площадь основания равна So=4*4=16 см². Площадь боковой поверхности в нашем случае равна
Sб=(1/2)*8*5=20 см².
Площадь полной поверхности: S=So+Sб=16+20=36см².
Объем правильной четырехугольной пирамиды равен (1/3)*So*h.
В нашем случае V=(1/3)*16*√21см³.
4. Найдите высоту правильной четырехугольной усеченной пирамиды, боковое ребро которой равно 16 см, а стороны оснований - 8 см и 4см.
Диагонали оснований (квадратов) усеченной пирамиды равны а√2, то есть D=8√2см и d=4√2см.
Опустим из любой вершины верхнего основания (например, А1) перпендикуляр А1Н на нижнее основание (этот перпендикуляр - высота нашей усеченной пирамиды) . Основание этого перпендикуляра Н будет лежать на диагонали D нижнего основания и расстояние от вершины нижнего основания до основания перпендикуляра АН будет равно (D-d)/2=2√2. Тогда искомую высоту найдем по Пифагору из прямоугольника АА1Н:
А1Н=√(АА1²-АН²)=√(16²-(2√2)²)= √248=2√62см.
5. Плоскость, параллельная основанию пирамиды, делит ее на два тела, объемы которых равны 128см³ и 96см³. В каком отношении эта плоскость делит высоту пирамиды?
Пусть указанная плоскость проходит через точку Р высоты SO пирамиды с объёмом V ( S – вершина пирамиды) и отсекает от данной пирамиды пирамиду с объёмом V1. Отсечённая пирамида подобна данной. Если k – коэффициент подобия, то V1/V=k³, так как отношение объемов подобных фигур равно кубу коэффициента подобия этих фигур. Объем исходной пирамиды равен сумме объемов двух тел: V=128+96=224cм³.
Тогда отношение объема V1 "верхней" пирамиды к объему V полной пирамиды равно 96/224=3/7. Значит отношение высоты SP "верхней" пирамиды к высоте SO исходной равно ∛(3/7). А отношение "верхней" части высоты пирамиды SP к ее "нижней" части PO равно ∛3/(∛7-∛3).