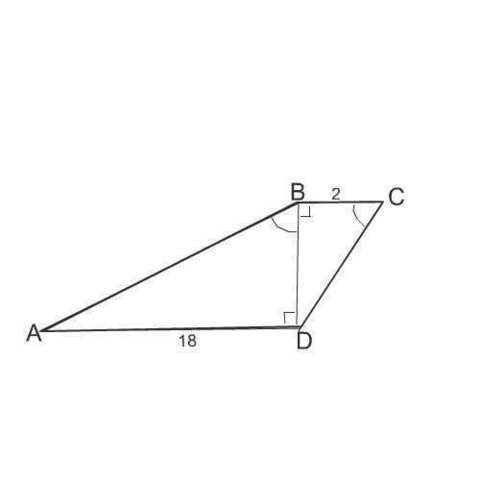
Сделаем рисунок и обозначим вершины трапеции АВСD.
Пусть основаниями будут ВС и АD.
По условию задачи ∠А+∠С=90º
Т.к. в треугольнике АВD ∠АВD+∠ВАD=90º, то ∠АВD= ∠ВСD
Если в прямоугольных треугольниках равны один из острых углов, то такие треугольники подобны.
Меньшая диагональ ВD является высотой трапеции - она перпендикулярна основаниям по условию.
Из подобия ᐃ АВD и ᐃ ВСD
АD:ВD=ВD:ВС
18:ВD=ВD:2
ВD²=36
ВD=6
Площадь трапеции равна половине произведения её высоты на сумму оснований.
S=6(2+18):2=60 ( квадратных единиц измерения)