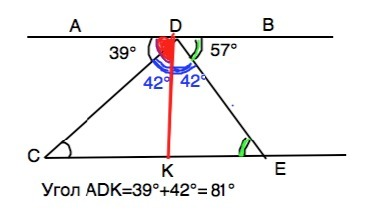
В треугольнике CDE ∠C= 39°, ∠E= 57°. Через вершину D проведена прямая AB параллельно CE.DK- биссектриса угла CDE. Найдите ∠ADK.
-------
АВ||СЕ, DC- секущая. ⇒
∠ADC=∠DCE=39° как накрестлежащие.
АВ|| СЕ, DE- секущая. ⇒
∠BDE=∠DEC=57° как накрестелжащие.
Угол АDB- развернутый и равен 180°
∠СDE=∠ADB - (∠ADC+∠BDE)=180°-96°=84°
Тогда, т.к. DK - биссектриса, ∠СDK=84°:2=42°
∠ADK=∠ADC+∠CDK=39°+42°=81°