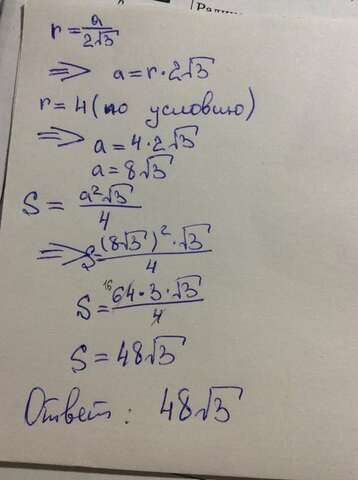Радиус вписанной в правильный треугольник окружности равен отношению его стороны к 2*(корень из трёх (далее буду обозначать как -/(3))), то есть: r=a/(2*(-/3)).
Следовательно, зная радиус, мы можем найти сторону: a=r*2*-/(3).
a=8-/(3).
Площадь S равностороннего треугольника (или правильного треугольника) равна ((a^2)*-/(3))/4.
Следовательно, S=(((8-/(3))^2)*-/(3))/4.
S=(64*3*-/(3))/4.
S=48*-/(3).
Ответ: 48*-/(3) - сорок восемь корней из трёх.
P. S.: чтобы было понятнее, постараюсь все вычисление прислать фотографией.