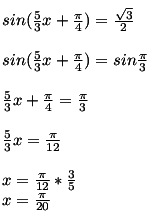1)sin(π/2-a)=cosa
2)sin(π-a)=sina
3)tg(180-a)=-tga
4)tg(180+a)=tga
5)cos(a+π/2)=-sina
6)см вложение
7)Заменим sinx=t
t∈[-1;1]
Получаем квадратное уравнение
6t^2-5t+1=0
D:25-24=1
t1=0.5
t2=1/3
Следовательно
sinx=0.5
x=(-1)^n*π/6+πn
sinx=1/3
x=arcsin1/3+2πn
x=π-arcsin1/3+2πk
8)Аналогично,замена tgx=t
2t^2-t-1=0
D:1+8=9
t1=1
t2=-0.5
tgx=1
x=π/4+πn
tgx=-0.5
x= -arctg(0,5) +πn
9)Снова замена
меняем arctgx на t
2t^2-t-3=0
D:1+24=25
t1=1.5
t2=-1
arctgx=1.5
arctgx=-1