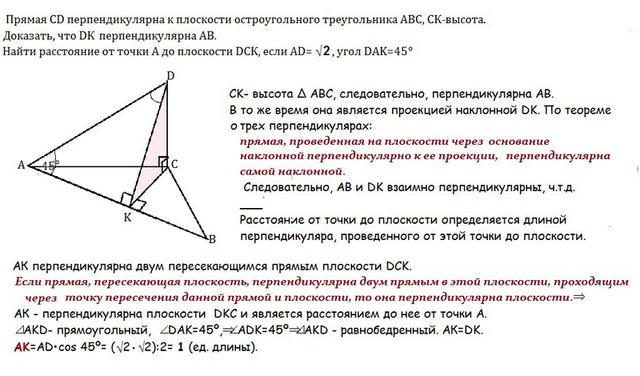
СK- высота ∆ АВС, следовательно, перпендикулярна АВ.
В то же время она является проекцией наклонной DK. По теореме о трех перпендикулярах:
прямая, проведенная на плоскости через основание наклонной перпендикулярно к ее проекции, перпендикулярна самой наклонной. Следовательно, АВ и DK взаимно перпендикулярны, ч.т.д.
___
Расстояние от точки до плоскости определяется длиной перпендикуляра, проведенного от этой точки до плоскости.
АК перпендикулярна двум пересекающимся прямым плоскости DCK.
Если прямая, пересекающая плоскость, перпендикулярна двум прямым в этой плоскости, проходящим через точку пересечения данной прямой и плоскости, то она перпендикулярна плоскости.⇒
АК - перпендикулярна плоскости DKC и является расстоянием до нее от точки А.
⊿ АKD- прямоугольный, ∠ DAK=45º,⇒∠ ADK=45º⇒
⊿ АKD - равнобедренный. АК=DK.
AK=AD•cos 45º= ( √2•√2):2=1 (ед. длины).