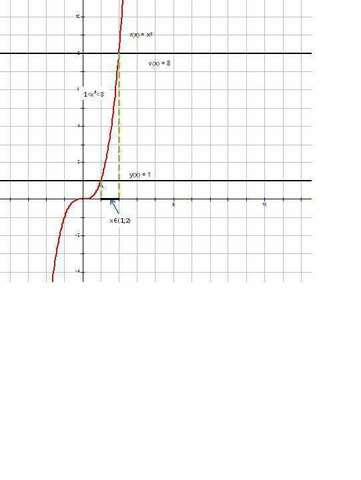
P(x)=x⁶-9x³+8
решить неравенство: Р(х)<0<br>x⁶-9x³+8<0<br>(x³)²-9*(x³)+8<0<br>замена переменных: x³=t
t²-9t+8<0 метод интервалов:<br>1. t²-9t+8=0. t₁=1, t₂=8
2.
+ - +
------(1)---------(8)------>t
t∈(1;8)
3. t>1, t<8<br>
обратная замена:
t>1. x³>1. x>1
t<8. x³<8, x³<2³. x<2<br>x∈(1;2)
ответ: нет наименьшего целого решения неравенства (по условию неравенство строгое)