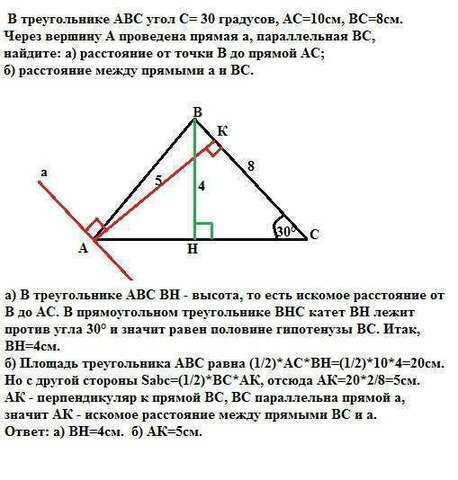
А) В треугольнике АВС ВН - высота, то есть искомое расстояние от В до АС. В прямоугольном треугольнике ВНС катет ВН лежит против угла 30° и значит равен половине гипотенузы ВС. Итак, ВН=4см.
б) Площадь треугольника АВС равна (1/2)*АС*ВН=(1/2)*10*4=20см.
Но с другой стороны Sabc=(1/2)*ВС*АК, отсюда АК=20*2/8=5см.
АК - перпендикуляр к прямой ВС, ВС параллельна прямой а, значит АК - искомое расстояние между прямыми ВС и а.
Ответ: а) ВН=4см. б) АК=5см.