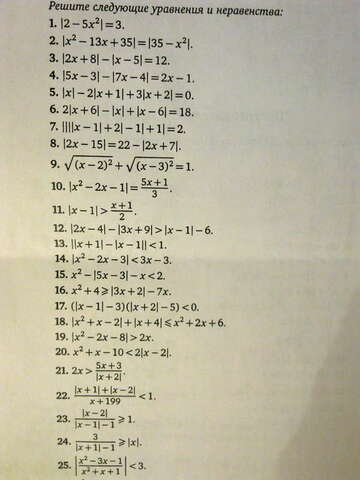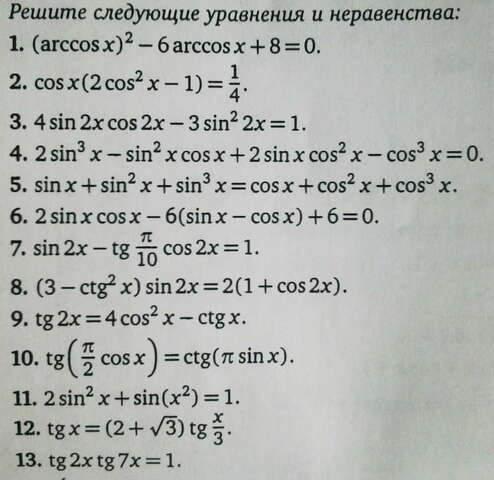ПОМОГИТЕ! ДАЮ МНОГО ПУНКТОВ! ПОЭТОМУ, ПОЖАЛУЙСТА, БУДТЕ ВНИМАТЕЛЬНЫ!
Нужно решить любые 5 тригонометрических уравнений, 3 уравнения с модулем и 5 неравенств с модулем. ЛЮБЫЕ. Все во вложении. Нужно срочно. Если не знаете, то лучше не пишите ерунду, пожалуйста. Желательно решение в виде фото. Если успеете решить больше, то буду очень благодарна! Пробовала решить сама, но ответы получаются либо кошмарные, либо корней вообще нет (но такого, наверное, просто не может быть). Очень надеюсь на вашу помощь