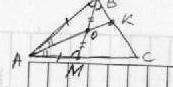
Пусть АВС - искомый треугольник, АК и ВМ - биссекирисы. Пусть биссектриса АК делит биссектрису ВМ пополам. Тогда по свойству биссектрисы треугольника: ВО/МО = АВ/АМ, так как ВО=МО (по условию), то АВ=АМ, а значит треугольник АВМ - равнобедренный, и ∠АВМ =∠АМВ, но так как ВМ - биссектриса ∠В и ∠АВМ = ∠МВС, то ∠АМВ = ∠МВС.
Но ∠АМВ - является внешним углом треугольника МВС и равен сумме двух углов несмежных с ним (∠АМВ = ∠МВС+∠МСК), что противоречит предыдущему выводу. Значит, не существует такого треугольника АВС