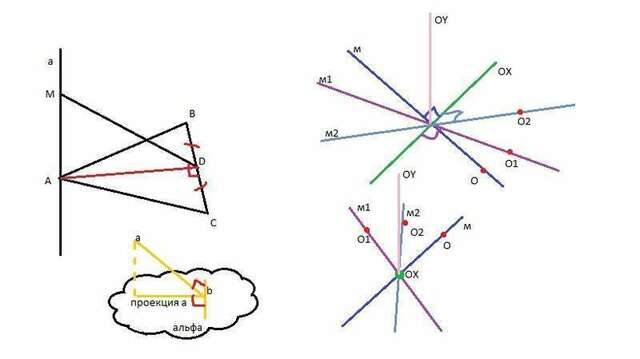
АD - это проекция гипотенузы MD на плоскость АВС. Поскольку MD перпендикулярна к BC, то ее проекция AD будет также перпендикулярна BC. Рассмотрим это поподробнее. Представим, что АВ - это ось ОХ, а MD - некая прямая м. Если прямая м перпендикулярна оси ОХ. Как бы мы не крутили эту прямую относительно оси ОХ, то есть, как бы мы не меняли значение координат Y и Z при постоянном значении Х, образовавшаяся прямая будет перпендикулярна оси ОХ). Например, есть некая точка О на прямой м. Всякий раз, когда будет изменяться значения Z и Y при постоянном значении X, образовавшаяся прямая будет перпендикулярна оси ОХ: O(x;y;z), O1(x;y1;z1), O2(x;y2;z2) ... On(x;yn;zn). Это можно выложить в одном предложении: если некая прямая а перпендикулярна прямой b, которая лежит на некой плоскости альфа, то проекция этой прямой на плоскость альфа будет перпендикулярна прямой b.
Из этих утверждений имеем: AD - это проекция MD (перпендикулярна ВС) на плоскость АВС, следовательно - АD перпендикулярна ВС. Далее, поскольку BD = DC, то АD является не только высотой треугольника АВС, а и его медианой. Треугольник, у которого высота является и медианой, является равнобедренным с равными углами при основе, на которую опущена высота (угол АВС равен углу АСВ), следовательно - треугольник АВС - равнобедренный: АВ = АС.