Отношение длин двух отрезков, каждый из которых соединяет точки параллельных плоскостей,...

Question

Отношение длин двух отрезков, каждый из которых соединяет точки параллельных плоскостей, равно 2:3.Эти отрезки с плоскостями составляют углы ,отношение которых равно 2.Найдите косинус большего из этих углов.

Answer 1

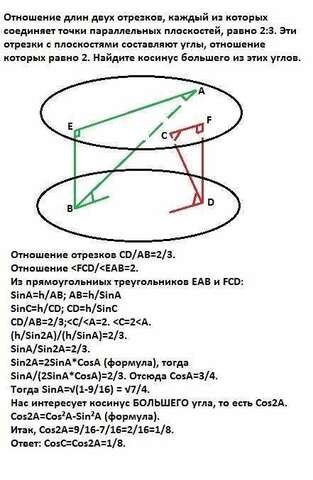
Отношение отрезков CD/АВ=2/3.
Отношение Из прямоугольниых треугольников ЕАВ и FСD:
SinA=h/AB; AB=h/SinA
SinC=h/CD; CD=h/SinC
CD/AB=2/3;<С/<А=2. <С=2<А.<br>(h/Sin2А)/(h/SinA)=2/3.
SinA/Sin2А=2/3.
Sin2A=2SinA*CosA (формула), тогда
SinA/(2SinA*CosA)=2/3. Отсюда CosA=3/4.
Тогда SinA=√(1-9/16) = √7/4.
Нас интересует косинус БОЛЬШЕГО угла, то есть Cos2A.
Cos2A=Cos²A-Sin²A (формула).
Итак, Cos2A=9/16-7/16=2/16=1/8.
Ответ: CosC=Cos2A=1/8.

---