Поначалу, узнаем область определения функции:
Так эта функция имеет смыл при всех значениях икс, то получаем:

Проверим на четность:
 - то функция четна.
- то функция четна.
 - то функция нечетна.
- то функция нечетна.
Если ни один из этих определений не работают в нашей функции. То наша функция будет не чётна, не нечётна.
Проверим:

Так как, степень четная, то получим:

Значит наша функция чётна, то есть, симметрична относительно оси игрек.
Найдем теперь производную:

Теперь найдем критические точки, при которых производная обращается в нуль:







Отметим данные точки, на числовой прямой, и определим знак производной на интервалах:





То есть наглядно, это выглядит так:
- + - +
-------- ---------
--------- ---------
--------- ---------->
---------->
Таким образом,  точка минимума, x=0 точка максимума,
точка минимума, x=0 точка максимума,  точка минимума.
точка минимума.



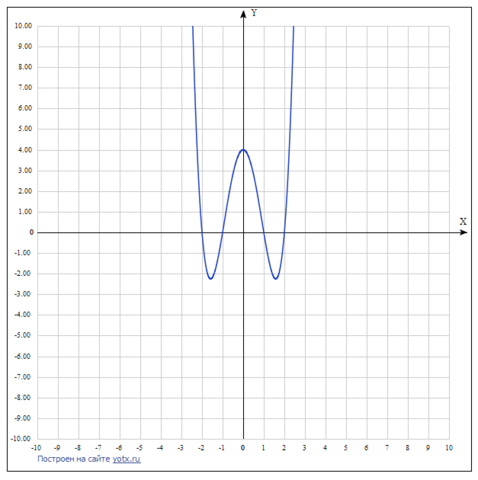
Теперь строим график, на основе проделанного исследования (во вложении)