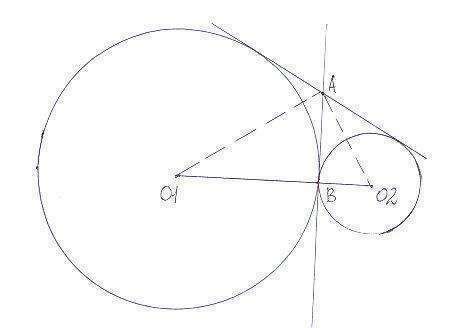
вот вам рисунок
Решение очень простое - вся "хитрость" в том, что угол О1АО2 (между пунктирными прямыми) равен 90 градусам. Дело в том, что О1А и О2А - биссеткриссы смежных углов (почему биссектрисы, - это понятно? обоснуйте), а сумма смежных углов 180 градусов. Ну, сумма половин смежных углов (то есть сумма угла О1АВ и угла О2АВ) дает 90.
Таким образом, трегольник О1АО2 - прямоугольный, и АВ - высота к гипотенузе.
Дальше - очень полезное "заклинание" - хотя и очень простое.
Высота к гипотенузе делит прямоугольный треугольник на два, подобные ему - и между собой тоже, конечно.
Поэтому
О1B/АВ = АВ/О2В;
О1B = АВ^2/O2B = 6^2/4 = 9;