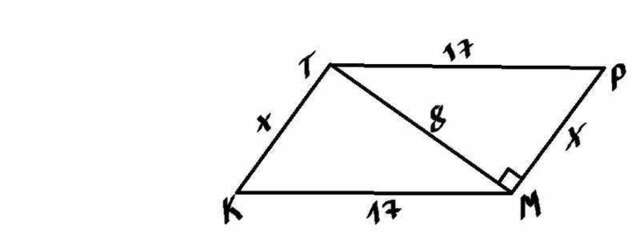
Обозначим вторую диагональ у. Мисленно дорисовуем ее на рисунке. Тогда, рассматриваем триугольник TMP. Он прямоугольний. Тогда за теоремой Пифагора x^2 + 8^2 = 17^2. А дальше применяем теорему Птолемея про соотношение сторон и диагоналей: x*x + 17*17 = 8*y. Имеем два уравнения откуда и находим y (y=64,25см). К задаче - рисунок.