Площадь полной поверхности прямого параллелепипеда равна сумме площади боковой поверхности и площади двух его оснований.
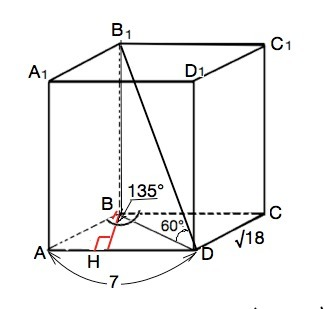
В прямом параллелепипеде АВСDD1A1B1C1 тупой угол основания 135°, ⇒острый, как внутренний односторонний с ним, равен 180°-135°=45°
Высота ВН прямоугольного ∆ АВD=AB•sin45°=√18•√2/2=3 см
S(ABCD)=ВН•AD=3•7=21 см²
BD - меньшая диагональ основания и является проекцией меньшей диагонали параллелепипеда.
ВD=√(BH²+HD*)=√(3•+(7-3)*)=5 см
Т.к. параллелепипед прямой, его высота равна боковому ребру.
ВВ1=ВD•tg60°=5√3 см
S(бок)=5√3•(2•7+2•√18)=5√3•(14+6√2)=70√3+30√6 или ≈194,728 см²
S(полн)=194,728+42=236,728 см²