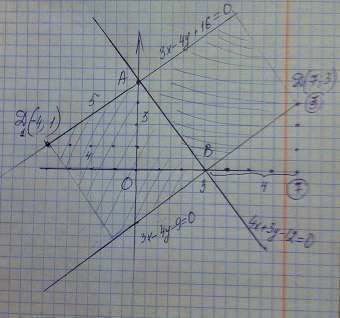
1) Найдем точки пересечения прямой 4х+3у-12=0 с координатными осями
х=0 тогда у= 4 А(0; 4)
у=0 тогда х=3 В(3;0)
2) Прямые перпендикулярные данной имеют вид 3х-4у+с=0
нормальные векторы взаимно перпендикулярных прямых ортогональны
нормальный вектор данной прямой (4;3)
нормальный вектор ортогональных прямых (3;-4)
Скалярное произведение в самом деле даст 0
4·3+3·(-4)=0
Чтобы найти с подставим координаты точек
А(0;4)
3·0-4·4+с=0 ⇒ с =16
3х-4у+16=0 уравнение прямой, перпендикулярной прямой 4х+3у-12=0 и проходящей через точку А
В(3;0)
3·3-4·0+с=0 ⇒ с = -9
3х-4у-9=0 уравнение прямой, перпендикулярной прямой 4х+3у-12=0 и проходящей через точку В
Сторона квадрата АВ=5 ( египетский треугольник)
Отложим на прямой 3х-4у-9=0 отрезок BD=5
Получим точку D
Координаты этой точки удобнее всего считать по клеточкам
D(7;3)
Уравнение прямой DС, параллельной АВ:
4х+3у+m=0
Чтобы найти m подставим координаты точки D
4·7+3·3+m=0 ⇒ m=-37
4x+3y-37=0 - уравнение прямой DC
Отложим на прямой 3х-4у+16=0 отрезок AC=5
Получим точку D₁
Координаты этой точки удобнее всего считать по клеточкам
D(-4;1)
Уравнение прямой D₁С, параллельной АВ:
4х+3у+m=0
Чтобы найти m подставим координаты точки D₁
4·(-4)+3·1+m=0 ⇒ m=13
4x+3y+13=0 - уравнение прямой DC