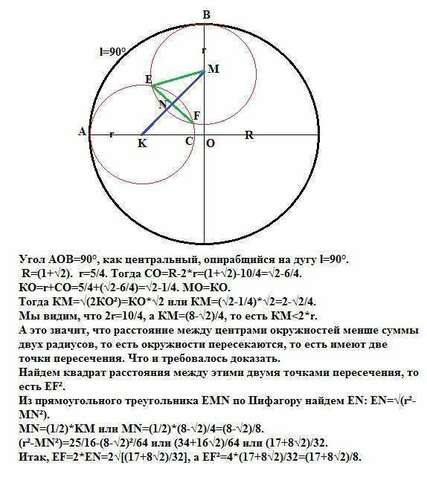
Дано: угол АОВ=90°, как центральный, опирающийся на дугу l=90°.
R=(1+√2). r=5/4. Тогда СО=R-2*r=(1+√2)-10/4=√2-6/4.
КО=r+CO=5/4+(√2-6/4)=√2-1/4. МО=КО.
Тогда КМ=√(2КО²)=КО*√2 или КМ=(√2-1/4)*√2=2-√2/4.
Мы видим, что 2r=10/4, a КМ=(8-√2)/4, то есть КМ<2*r.<br>А это значит, что расстояние между центрами окружностей меньше суммы двух радиусов, то есть окружности пересекаются,
а значит имеют две точки пересечения.
Что и требовалось доказать.
Найдем квадрат расстояния между этими двумя точками пересечения, то есть EF².
Из прямоугольного треугольника EMN по Пифагору найдем ЕN: EN=√(r²-MN²).
MN=(1/2)*KM или MN=(1/2)*(8-√2)/4=(8-√2)/8.
(r²-MN²)=25/16-(8-√2)²/64 или (34+16√2)/64 или (17+8√2)/32.
Итак, ЕF=2*EN=2√[(17+8√2)/32], а ЕF²=4*(17+8√2)/32=(17+8√2)/8.