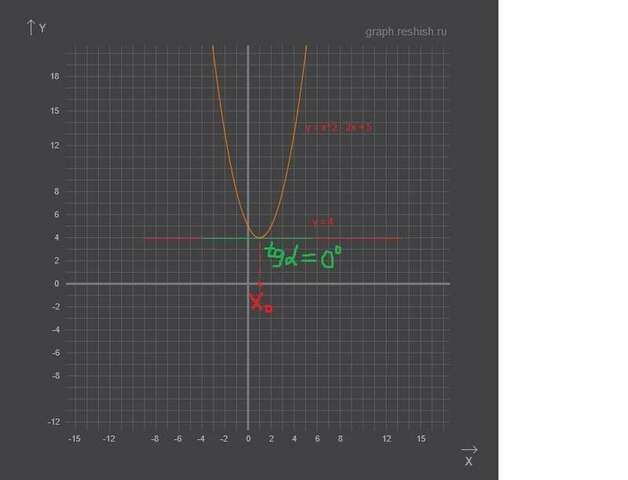
Уравнение касательной к графику функции: y = f(x0) + f'(x0)*(x-x0). Найдем это уравнение. x0 = 1; f(x0) = 1^2 - 2*1+5 = 1 - 2 +5 = 4; производная f'(x0) = 2x - 2; производная в точке x0: f'(x0) = 2*1 - 2 = 0. Подставим же эти значения: y = 4 + 0*(x-1); y = 4.
Ответ: y = 4.
Для того, чтобы найти угол наклона касательной к графику функции, нужно найти тангенс угла наклона. Тангенс угла наклона касательной к графику функции в точке x0 равен производной функции в точке х0. Имеем: f'(х0) = 2x - 2; f'(1) = 2*1 - 2; f'(1) = 0. Тангенс угла наклона равен 0. Угол, тангенс которого равен 0 - 0 градусов. Ответ: угол наклона касательной к данной параболе в точке х0 равен 0 градусов.