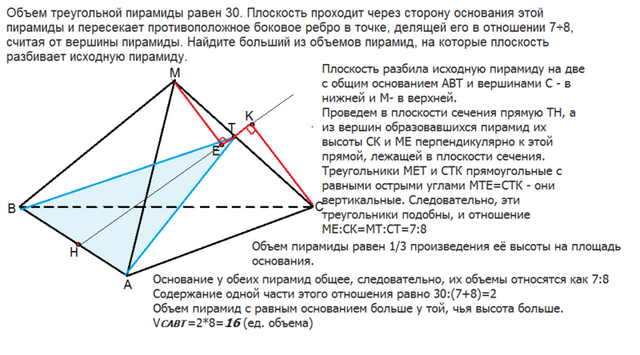
Пусть данная пирамида будет МАВС, а сечение её плоскостью - АВТ.
МТ:ТС=7:8
Плоскость разбила исходную пирамиду на две с общим основанием АВТ и вершинами С - в нижней и М- в верхней.
Проведем в плоскости сечения прямую ТН, а из вершин образовавшихся пирамид их высоты СК и МЕ перпендикулярно к этой прямой, лежащей в плоскости сечения, а значит и перпендикулярно плоскости их общего основания.
Треугольники МЕТ и СТК прямоугольные с равными острыми углами МТЕ=СТК - они вертикальные.
Следовательно, эти треугольники подобны, и отношение их высот равно отношению их сторон, т.е.
МЕ:СК=МТ:СТ=7:8
Объем пирамиды равен 1/3 произведения её высоты на площадь основания.
Основание у обеих пирамид общее, следовательно, их объемы относятся как 7:8
Содержание одной части этого отношения равно 30:(7+8)=2
Объем пирамид с равным основанием больше у той, чья высота больше.
V САВТ=2*8=16 (ед. объема)