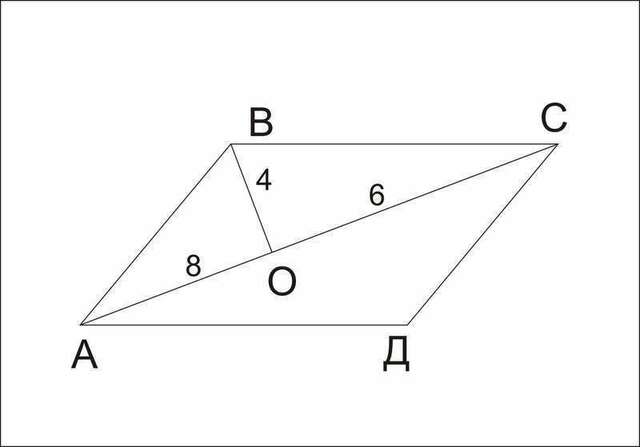
Диагональ АС делит параллелограмм на два равных треугольника:
АВС и АДС
( АД=ВС, АВ=СД, АС – общая: третий признак равенства
треугольников. По трем сторонам).
Рассмотрим треугольник АВС: АС=АО+ОС=8+6=14
Найдем площадь треугольника АВС:
Формула площади треугольника: S=1/2*a*h (где a –
основание треугольника, h – высота треугольника).
Sabc=1/2*АС*ВО=1/2*14*4=28
кв. ед.
Так как треугольники АВС и АДС равны, то площадь
параллелограмма АВСД будет равна:
Sabcд=Sabc*2=28*2=56 кв. ед.