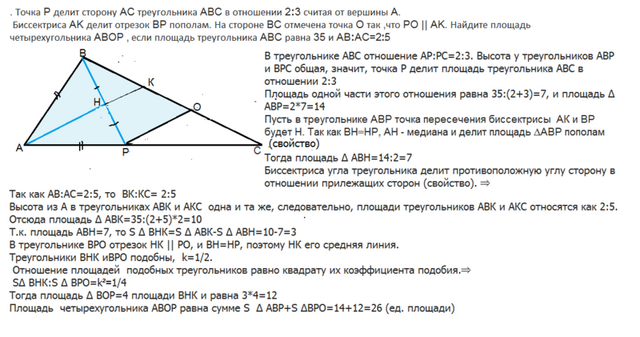
В треугольнике АВС отношение АР:РС=2:3.
Высота у треугольников АВР и ВРС общая, значит, точка Р делит площадь треугольника АВС на два в отношении 2:3
Площадь одной части этого отношения равна 35:(2+3)=7, и площадь
∆ АВР=2*7=14
Пусть в треугольнике АВР точка пересечения биссектрисы АК и отрезка ВР будет Н.
Так как ВН=НР, АН - медиана и делит площадь ∆АВР пополам (свойство).
Тогда площадь ∆ АВН=14:2=7
Биссектриса угла треугольника делит противоположную углу сторону в отношении прилежащих сторон (свойство). ⇒
Так как АВ:АС=2:5, то ВК:КС= 2:5
Высота из А в треугольниках АВК и АКС одна и та же, следовательно, площади треугольников АВК и АКС относятся как 2:5.
Отсюда площадь ∆ АВК=35:(2+5)*2=10
Т.к. площадь АВН=7, то Ѕ ∆ ВНК=Ѕ ∆ АВК-Ѕ ∆ АВН=10-7=3
В треугольнике ВРО отрезок НК || РО, и ВН=НР, поэтому НК его средняя линия. Треугольники ВНК иВРО подобны, k=1/2.
Отношение площадей подобных треугольников равно квадрату их коэффициента подобия.⇒
Ѕ∆ ВНК:Ѕ ∆ ВРО=k²=1/4
Тогда площадь ∆ ВОР=4 площади ВНК и равна 3*4=12
Площадь четырехугольника АВОР равна
Ѕ ∆ АВР+Ѕ ∆ВРО=14+12=26 (ед. площади)