1) Постройте треугольник с помощью сторон; а=3,b=8 b c=9,
Все делайте точно по алгоритму вложения 1. Получите треугольник , и именно тот, что нужен. ( По тому же принципу дано построение в конце решения - пункт 5 задания)
2)
A) Можно ли построить треугольник со сторонами a=3.b=4 и c=7
Нельзя.
Сумма длин любых двух сторон треугольника должна быть больше длины третьей стороны.
(Иначе получится не треугольник, а "складной метр").
3+4=7.
"Вершина", которая должна получиться при пересечении сторон 3 и 4, будет находиться на отрезке, равном 7.
B) Какому условию должны удовлетворять длины отрезков a, b и c для того, чтобы быть длинами сторон треугольника?
Об этом условии сказано в ответе на предыдущий вопрос.
Сумма длин любых двух сторон треугольника должна быть больше длины третьей стороны.
3) Постройте прямоугольный треугольник по 2 катетам
Расскажу и покажу, как это сделать. Смотрите вложение.
Катеты должны составлять прямой угол.
Поэтому чертим горизонтальную прямую.
С помощью циркуля и линейнки проводим к ней перпендикуляр.
Делается это очень просто.
Произвольным раствором циркуля из произвольной точки О на этой прямой чертим полуокружность.
Тем же раствором циркуля с центром О1 в другой точке прямой чертим другую полуокружность, чтобы обе пересеклись по обе стороны прямой.
Точки пересечения соединяем.
Получился отрезок PQ, перпендикулярный первой прямой.
На прямой откладываем раствором циркуля (1 - зеленого цвета на моем рисунке)
с центром в точке С отрезок, равный длине одного катета СА.
На перпендикуляре - раствором циркуля (2- голубого цвета на рисунке), равным длине второго катета, из центра в той же точке С откладываем отрезок СВ, равный второму катету.
Точки пересечения полуокружностей и прямых - концы отрезков - соединяем. Треугольник построен.
4) Постройте прямоугольный треугольник по гипотенузе и катету
Все то же самое.
Только один отрезок, например, СА, равен длине катета,
его откладываем на прямой.
Затем из этого конца А как центра окружности, раствором циркуля, равным длине гипотенузы (на рисунке - полуокружность розового цвета),
чертим полуокружность до пересечения с построенным раньше перпендикуляром PQ. Точку пересечения В полуокружности c прямой PQ и точку А соединим.
Получен прямоугольный треугольник по катету и гипотенузе.
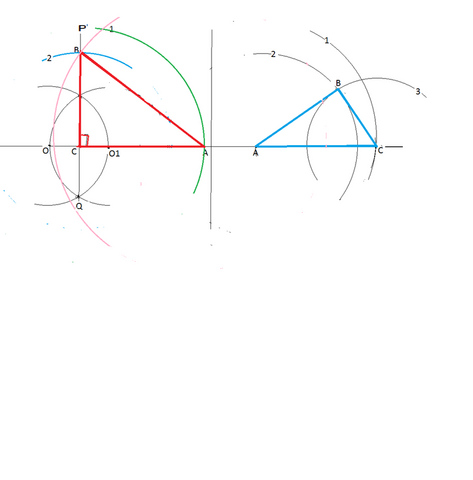
5) Дана прямая a . Постройте треугольник, равный ABC, изображенному на рисунке 6, так чтобы одна его сторона лежала на прямой a.
Строим.
Для построения нужны циркуль, линейка, карандаш.
Измерьте циркулем длинную ( горизонтальную ) сторону АС данного на рисунке треугольника.
Отложите эту длину этим же раствором циркуля на прямую с центром в произвольной точке А.
Точку пересечения полуокружности с прямой обозначьте С.
Из точки А раствором циркуля, равным длине второй стороны АВ ,
начертире полуокружность ( на рисунке под номером 2).
Из центра в точке С раствором циркуля, равным длине третьей стороне СВ, начертите полуокружность (3)
до пересечения с полуокружностью (2).
Эта точка пересечения - третья вершина треугольника -
вершина угла С.
Соединив все три точки, получите треугольник, равный данному.
Вложение 1.
Здесь понятно все. Руководствуясь данными в нем подсказками, сумеете построить треугольник без труда.
Вложение 2.
Делаете то, что написано во вложении 1, и треугольник будет построен.
1)Сначала откладываете на прямой отрезок, равный 5. Отмечаем концы отрезка АС
2)Затем раствором циркуля, равным 3, с центром в точке А, чертите полуокружность.
3) Раствором циркуля, равным 4, с центром в другом конце С отрезка, чертите вторую полуокружность. В точке пересечения будет третья вершина В треугольника.
Вложение 3. Построение по этому рисунку уже сделано выше.
---------------------------------------------------------------------------
Чтобы было удобно одновременно читать решение и смотреть рисунки, кликните правой кнопкой и нажмите курсором "Открыть ссылке в отдельном окне". Затем перетащите это окно отдельно, свернув каждую страницу - решение и рисунок - в отдельное окно. Они будут рядом, что удобно, т.к. рисунок не будет заслонять решение.