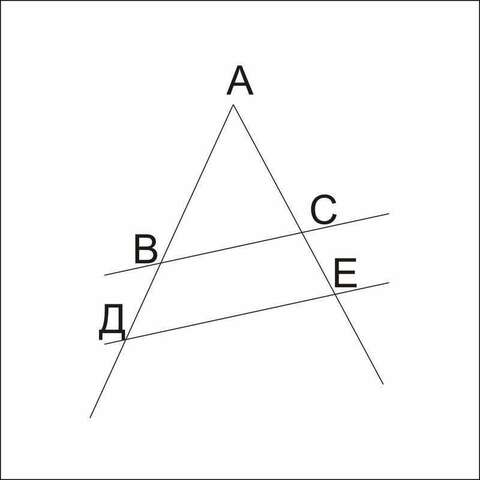
Рассмотрим
получившиеся треугольники АВС и АДЕ:
Угол А – общий. Углы
АВС и АДЕ равны как соответственные
углы образованные параллельными
прямыми, пересеченными секущей
Значит данные
треугольники подобны по первому признаку подобия треугольников: Если два угла одного треугольника
соответственно равны двум углам другого треугольника, то треугольники подобны.
Сторона АЕ треугольника
АДЕ равна АС+СЕ:
АЕ=8+4=12 см.
Зная это, мы можем
найти коэффициент подобия треугольников:
k=АЕ/АС=12/8=1,5
Найдем стороны треугольника
АДЕ:
АД=АВ*k=10*1.5=15 см.
ДЕ=ВС*k=4*1,5=6 см.
ВД=АД-АБ=15-10=5 см.
Ответ: ВД=5 см. ДЕ=6 см.