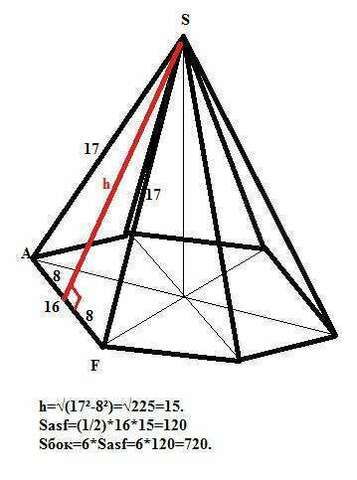
Боковая поверхность данной пирамиды равна сумме площадей шести равнобедренных треугольников с основанием 16 и боковой стороной 17. Не будем пользоваться готовой формулой. Найдем апофему (высоту) боковой грани по Пифагору: h=√(17²-8²)=15.
Тогда площадь боковой грани Sг=(1/2)*16*15=120. А площадь боковой поверхности пирамиды равна 6*120=720 ед².