Это, наверное, трудный способ, но другого в голову не идет.
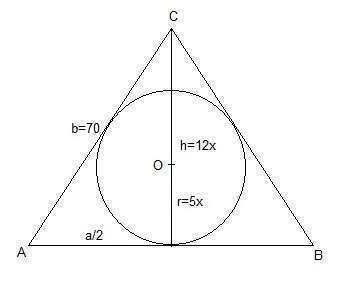
У равнобедренного треугольника боковая сторона b = 70.
Центр вписанной окружности делит высоту h в отношении 7:5.
Это значит, что высота h = 12x, радиус впис. окр. r = 5x.
Основание а можно узнать из теоремы Пифагора.
(a/2)^2 = b^2 - h^2 = 4900 - 144x^2
a = 2√(4900 - 144x^2)
Периметр треугольника P = a + 2b = 2√(4900 - 144x^2) + 140
Площадь треугольника, с одной стороны, равна
S = a*h/2 = 2√(4900 - 144x^2)*12x/2 = 12x*√(4900 - 144x^2)
С другой стороны, эта же площадь равна
S = P*r/2 = (√(4900 - 144x^2) + 70)*5x
Можно приравнять
5x*√(4900 - 144x^2) + 5x*70 = 12x*√(4900 - 144x^2)
5x*70 = 7x*√(4900 - 144x^2)
Делим на 7x
√(4900 - 144x^2) = 50
4900 - 144x^2 = 2500
x^2 = (4900 - 2500)/144 = 2400/144 = 200/12 = 100/6
x = 10/√6 = 10√6/6
h = 12x = 12*10√6/6 = 20√6
a =
2√(4900 - 144x^2) = 2√(4900 - 144*100/6) = 2√(2500) = 100
S = a*h/2 = 100*20√6/2 = 1000√6