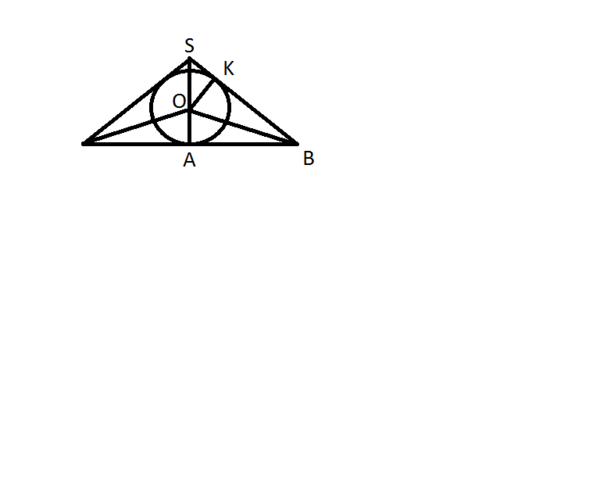
Рассмотрим треугольник одна вершина которого совпадает с вершиной пирамиды, а две другие - середины противолежащих сторон основания
SA = SB * sin ABS
SB = AB / cos ABS
AB = OB * cos ABO
OB = AO / sin ABO
учитывая, что AO = 1 по условию
AB = 2 (половина стороны основания)
2 = AB = OB * cos ABO = (AO / sin ABO) * cos ABO = cos ABO / sin ABO
или cos ABO = 2 sin ABO
угол ABS в два раза больше ABO. Поэтому по формулам преобразования двойных углов получим
SA = SB * sin ABS = (AB / cos ABS) * sin ABS =
= (2 / (cos^2 ABO - sin^2 ABO)) * 2 sin ABO cos ABO =
(подставим здесь формулу cos ABO = 2 sin ABO)
= 4 sin ABO (2 sin ABO) / (4 sin^2 ABO - sin^2 ABO) =
=8 sin^2 ABO / (3 sin^2 ABO) = 8/3
Объем пирамиды равен 1/3 hS = 1/3 * 8/3 * 4*4 = 128/9 =