Как известно, высота равнобедренной трапеции, диагонали которой взаимно перпендикулярны, равна её средней линии ( полусумме оснований).
Тогда h=(8+10):2=9 см
S=0,5•(8+10)•9=81 см²
---------------
Подробнее:
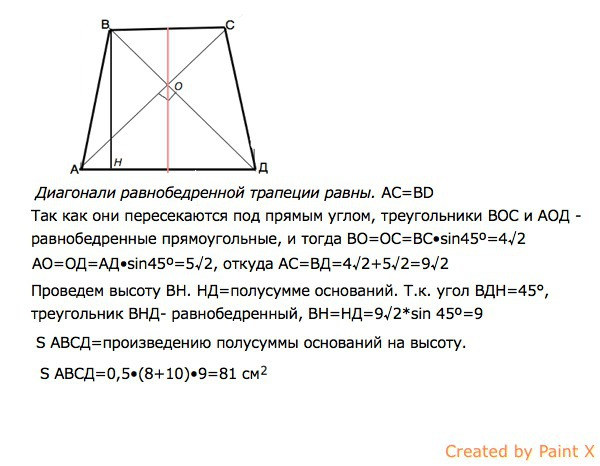
Диагонали равнобедренной трапеции равны. AC=BD
Так как они пересекаются под прямым углом, треугольники ВОС и АОД - равнобедренные прямоугольные, и тогда ВО=OC=ВС•sin45º=4√2 AO=OД=АД•sin45º=5√2, откуда
АС=ВД=4√2+5√2=9√2
Проведем высоту ВН.
НД=полусумме оснований (свойство равнобедренной трапеции)
. Т.к. угол ВДН=45°, треугольник ВНД- равнобедренный, ВН=НД=9√2*sin 45º=9
S АВСД=произведению полусуммы оснований на высоту.
S АВСД=0,5•(8+10)•9=81 см²