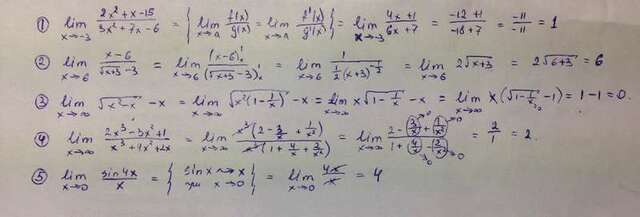Теорема (правило Лопиталя). Пусть функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a, и пусть или . Тогда, если существует предел отношения производных этих функций , то существует и предел отношения самих функций f(x)/g(x) при x→а, причем .
Другими словами надо взять отдельно производную от числителя и знаменателя, и предел от производных будет равен первоначальному пределу.
_______________________________________________________________________
Не видел комментария и поэтому уже решил правилом Лопиталя, но там есть 3 решенных примера по другим свойствам пределов.