Если вы полагаете, что
 то это большое заблуждение!
то это большое заблуждение!
Давайте в этом разберёмся!
Действие возведения в квадрат – точно соответствует нахождению площади квадрата со стороной, длина которой равна числу, возводимому в квадрат. Ну, например, мы хотим возвести в квадрат  понятно, что
понятно, что  но мы не будем сразу возводить
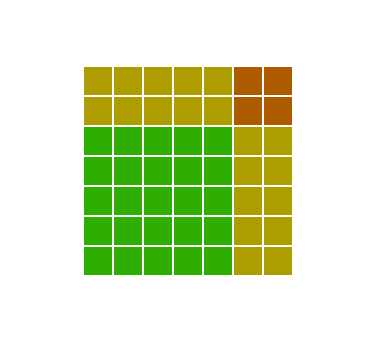
но мы не будем сразу возводить  в квадрат, а попробуем разобраться в этом графически. Взглянем на рисунок (приложен к объяснению)
в квадрат, а попробуем разобраться в этом графически. Взглянем на рисунок (приложен к объяснению)
Как мы видим, если мы сложим только  (это зелёный квадрат) и
(это зелёный квадрат) и  (это оранжевый квадрат), то мы не получим площадь квадрата со стороной
(это оранжевый квадрат), то мы не получим площадь квадрата со стороной  Чтобы получить правильную сумму
Чтобы получить правильную сумму  необходимо прибавить ещё два жёлтых прямоугольника с площадями
необходимо прибавить ещё два жёлтых прямоугольника с площадями 
Тогда получиться, что:
 ;
;
Ну и так же легко проверить, что:
 ;
;
А вот:  потому:
потому:  ;
;
Если бы мы проводили такие рассуждения не для  и
и  а для каких-то любых
а для каких-то любых  и
и  то получилось бы всё аналогично:
то получилось бы всё аналогично:
 ;
;
Итак:  ;
;
Тоже самое можно доказать и аналитически (алгебраически), если предварительно обозначить как  :
:

 ;
;
Если вы всё уловили, то вам не сложно будет доказать аналитически, что:
 ;
;
Для разности тоже можно изобразить иллюстрацию с площадями, но она получится более путанной и в ней тяжелее разобраться, чем доказывать разность аналитически. Но разобраться можно, и она, конечно же, полностью соответствует формулам, представленным выше.
Для вашей конкретной ситуации получим:

 ;
;

 ;
;
Но вообще, я бы рекомендовала, решать данную задачу совсем через другую формулу!
Есть такая формула  формула [2] ;
формула [2] ;
Это легко доказать так 
 ;
;
Так что, теперь воспользуемся формулой [2] в вашем случае и получим:
 ;
;
 ;
;
Обозначим  и
и  тогда:
тогда:



 ;
;
Значит:  что возможно только если выражение в скобках равна нулю, т.е.:
что возможно только если выражение в скобках равна нулю, т.е.:
 ;
;
 ;
;

О т в е т :