В треугольнике авс угол с =90,sin a =7/√113,найти tg А. И еще одну задачку, даю 30...

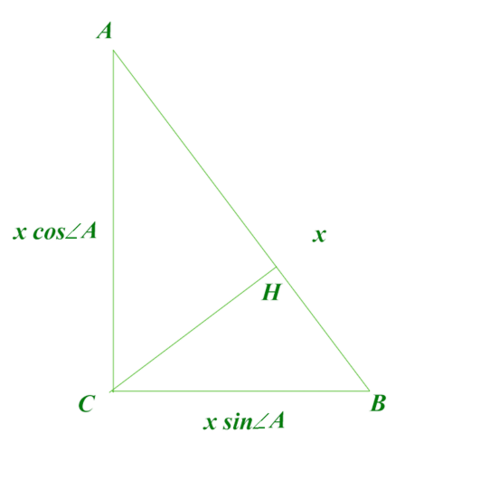
№ 1 .

Поскольку задача по геометрии, и дан треугольник, то, видимо, подразумевается, что она должна быть решена не в рамках алгебраических тождеств, а с помощью геометрических рассуждений:

Итак, нам не известна длина сторон треугольника, зададим тогда одну их сторон через неопределённое число. Пусть гипотенуза $AB ,$ лежащая напротив угла $\angle C$ – это $AB = x ,$ тогда:

$CB = x \sin{ \angle A }$ ;

$CB = x \cdot \frac{7}{ \sqrt{113} }$ ;

$CB = \frac{7}{ \sqrt{113} } x$ ;

Теперь по теореме Пифагора найдём $AC = \sqrt{ AB^2 - BC^2 }$ ;

$AC = \sqrt{ x^2 - ( \frac{7}{ \sqrt{113} } x )^2 } = \sqrt{ x^2 - x^2 ( \frac{7}{ \sqrt{113} } )^2 } =$

$\sqrt{ x^2 ( 1 - \frac{7^2}{ ( \sqrt{113} )^2 } ) } = x \sqrt{ 1 - \frac{49}{113} } = x \sqrt{ \frac{64}{113} }$ ;

$AC = \frac{8}{ \sqrt{113} } x$ ;

Теперь, как раз и найдём $tg{ \angle C } .$

$tg{ \angle A } = \frac{CB}{AC} = \frac{7}{ \sqrt{113} } x : ( \frac{8}{ \sqrt{113} } x ) = \frac{7x}{ \sqrt{113} } \cdot \frac{ \sqrt{113} }{8x} = \frac{7}{1} \cdot \frac{1}{8}$ ;

О т в е т : $tg{ \angle A } = \frac{7}{8} .$

№ 2 .

В рассуждениях 2-ой задачи используется тот же рисунок.

Треугольники $\Delta CBH$ и $\Delta ACH$ – подобны с точностью до перечисления вершин (начинаем с острого угла по гипотенузе), т.е.:

$\Delta CBH \sim \Delta ACH$ ;

Отсюда следует, что:

$\frac{BH}{HC} = \frac{HC}{HA} ,$ а значит:

$BH \cdot HA = HC \cdot HC$ ;

$HC^2 = BH \cdot HA$ ;

$HC = \sqrt{ BH \cdot HA }$ ;

$HC = \sqrt{ 2 \cdot 8 } = \sqrt{16}$ ;

О т в е т : $HC = 4 .$