В задаче сказано, что покупатель ходит по магазинам и прекращает шоппинг сразу, как только он покупает нужный товар. Однако есть важная оговорка, а именно о том, что возможных магазинов только пять! А это означает, что как только он пройдёт по пяти магазинам – он так же прекращает свой шоппинг, т.е. из заданного алгоритма есть два выхода, описанных в задаче: первое – выход с товаром из любого магазина, включая пятый; и второй – выход из пятого магазина без товара.
Вероятность того, что покупатель найдёт товар в первом магазине и прекратит шоппинг составляет  ;
;
Вероятность того, что покупатель найдёт товар во втором магазине, не найдя его в первом, и прекратит шоппинг составляет  ;
;
Вероятность того, что покупатель найдёт товар в третьем магазине, не найдя его в первых двух, и прекратит шоппинг составляет  ;
;
Вероятность того, что покупатель найдёт товар в четвёртом магазине, не найдя его в первых трёх, и прекратит шоппинг составляет  ;
;
Вероятность того, что покупатель прекратит шоппинг только после пятого магазина, вне зависимости от того нашёл он товар или нет, может быть найдена вычитанием из единицы всех остальных вероятностей:

 ;
;
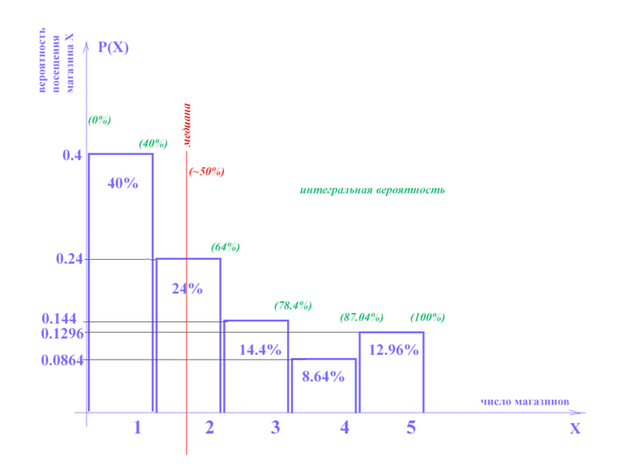
Закон распределения случайной величины таков:

Диаграмма распределения представлена на рисунке
Самое «модное» в распределении значение – один магазин. Таких людей  Мода
Мода  ;
;
Важно понимать, что у магазинов нет номеров, говоря о первом, третьем и т.п. магазинах, подразумевается не какой-то конкретный первый или третий магазин, а просто количество магазинов, которые по счёту посетил покупатель, и в том числе, какой по счёту магазин он посетил последним. На рисунке зелёным просуммирована интегральная вероятность. Так, например, положение и числовое значение  на диаграмме означает, что успешных шопперов, которые нашли товар не позднее третьего магазина –
на диаграмме означает, что успешных шопперов, которые нашли товар не позднее третьего магазина –  Ясно, что
Ясно, что  самых успешных – это шопперы, которые нашли товар в первом или втором магазине. Таким образом, Медиана
самых успешных – это шопперы, которые нашли товар в первом или втором магазине. Таким образом, Медиана  ;
;
Математическое ожидание, т.е. среднее число магазинов, посещаемых всеми подобными шопперами, находится как средне-взвешенное всех магазинов по их вероятностям, т.е.
![M[X] = P_1 \cdot 1 + P_2 \cdot 2 + P_3 \cdot 3 + P_4 \cdot 4 + P_5 \cdot 5 = M[X] = P_1 \cdot 1 + P_2 \cdot 2 + P_3 \cdot 3 + P_4 \cdot 4 + P_5 \cdot 5 =](https://tex.z-dn.net/?f=+M%5BX%5D+%3D+P_1+%5Ccdot+1+%2B+P_2+%5Ccdot+2+%2B+P_3+%5Ccdot+3+%2B+P_4+%5Ccdot+4+%2B+P_5+%5Ccdot+5+%3D+)


 ;
;
![M[X] = 2.3056 M[X] = 2.3056](https://tex.z-dn.net/?f=+M%5BX%5D+%3D+2.3056+) , т.е., говоря «по-русски», в средем эти шопперы посещают
, т.е., говоря «по-русски», в средем эти шопперы посещают  «магазина» ;
«магазина» ;
Дисперсию, или среднеквадратичное отклонение найдём, как средне-взвешенное квадратичное по вероятностям магазинов отклонение от мат.ожидания:
![D^2[X] = P_1 \cdot ( M[X] - 1 )^2 + P_2 \cdot ( M[X] - 2 )^2 + P_3 \cdot ( M[X] - 3 )^2 + D^2[X] = P_1 \cdot ( M[X] - 1 )^2 + P_2 \cdot ( M[X] - 2 )^2 + P_3 \cdot ( M[X] - 3 )^2 +](https://tex.z-dn.net/?f=+D%5E2%5BX%5D+%3D+P_1+%5Ccdot+%28+M%5BX%5D+-+1+%29%5E2+%2B+P_2+%5Ccdot+%28+M%5BX%5D+-+2+%29%5E2+%2B+P_3+%5Ccdot+%28+M%5BX%5D+-+3+%29%5E2+%2B+)
![+ P_4 \cdot ( M[X] - 4 )^2 + P_5 \cdot ( M[X] - 5 )^2 = + P_4 \cdot ( M[X] - 4 )^2 + P_5 \cdot ( M[X] - 5 )^2 =](https://tex.z-dn.net/?f=+%2B+P_4+%5Ccdot+%28+M%5BX%5D+-+4+%29%5E2+%2B+P_5+%5Ccdot+%28+M%5BX%5D+-+5+%29%5E2+%3D+)



 ;
;
Соответственно ![D[X] = \sqrt{ D^2[X] } = \sqrt{1.96260864} \approx 1.40093 D[X] = \sqrt{ D^2[X] } = \sqrt{1.96260864} \approx 1.40093](https://tex.z-dn.net/?f=+D%5BX%5D+%3D+%5Csqrt%7B+D%5E2%5BX%5D+%7D+%3D+%5Csqrt%7B1.96260864%7D+%5Capprox+1.40093+) , т.е., говоря «по-русски», среднее отклонение у разных шопперов от центрального значения
, т.е., говоря «по-русски», среднее отклонение у разных шопперов от центрального значения  «магазина» составляет
«магазина» составляет  «магазина», т.е.
«магазина», т.е. 
О т в е т:  ;
;
![M_o = 1 ; M_e = 2 ; M[X] = 2.3056 ; D[X] \approx 1.40093 . M_o = 1 ; M_e = 2 ; M[X] = 2.3056 ; D[X] \approx 1.40093 .](https://tex.z-dn.net/?f=+M_o+%3D+1+%3B+M_e+%3D+2+%3B+M%5BX%5D+%3D+2.3056+%3B+D%5BX%5D+%5Capprox+1.40093+.+)