Помогите пожалуйста с геометрией!)

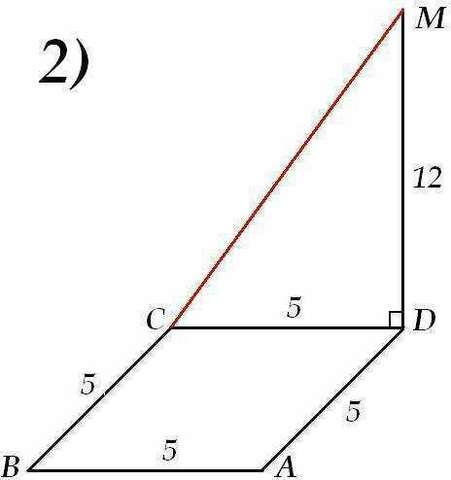
2) По т. Пифагора находится:
$MC=\sqrt{DM^2+CD^2}=\sqrt{12^2+5^2}= \sqrt{144+25}= \sqrt{169}=13$ см

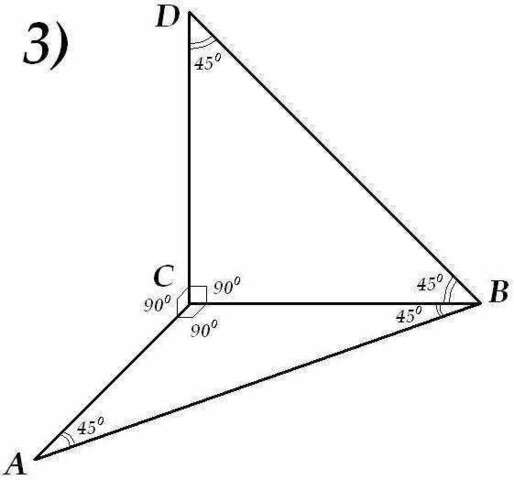
3) Рисунок во вложении, в принципе всё понятно:
В равнобедренных прямоугольных треугольниках острые углы при основании равны 45° (всё обозначено на рисунке). Угол между прямой BD и плоскостью АВС - это угол между BD и её проекцией на плоск. АВС. Этой проекцией является ВС.
∠DBC=45° - и есть искомый угол.

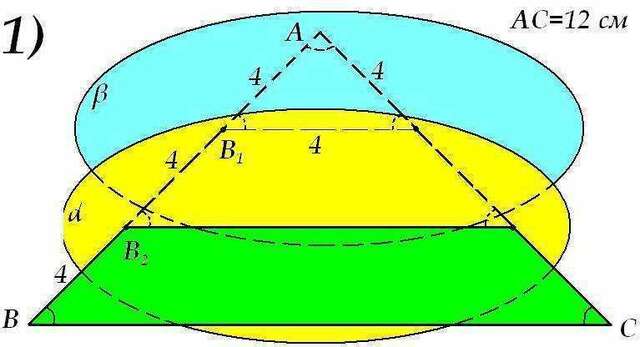
1) Не совсем понятно, правда, зачем в условии вся эта заморочка с плоскостями, можно было и параллельными отрезками обойтись.
Если ΔАВС - равносторонний, то АВ=ВС=АС=12 см
Также, если $AB_1=B_1B_2=B_2B$ , то

$AB_1=B_1B_2=B_2B= \frac{AB}{3}= \frac{12}{3}=4$ см

Если по условию плоскости $\alpha$ и $\beta$ параллельны ВС, то все острые углы на рисунке равны 60°, значит все треугольники подобны и равносторонние.
Все стороны нужного нам треугольника равны 4, значит
$P=3\cdot4=12$ см