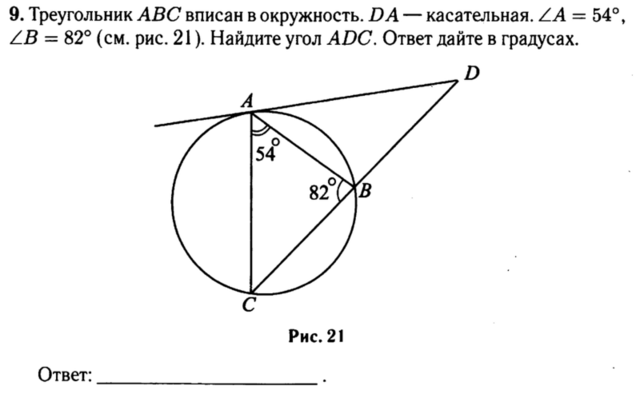
Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами ⇒
∠АDС=(◡ АС-◡АВ):2
Угол АВС вписанный и равен половине дуги АС, на которую он опирается ⇒
Дуга АС =2*82º=164º
Угол АСВ вписанный и равен половине дуги АВ, на которую он опирается.
Угол АСВ=180º-(54º+82º)=44 ⇒
Дуга АВ=2*44º=88ºУгол АDC= (164 -88):2=38º
-----------------------
Можно использовать и другое свойство углов, связанных с окружностью. Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами. ⇒
угол ВАD= углу АСВ, равному половине дуги АВ
Угол АВD смежный углу АВС и равен 180º-82º=98º
Тогда из треугольника АВD следует:
Угол АDB=180º-(98º+44º)=38º