4.2.1.
По теореме Пифагора квадрат гипотенузны равен сумме квадратов двух катетов.
Пусть гипотенуза с,тогда
с²=40²+9²=1600+81=1681
с=√1681=41
4.2.2
Применим теорему Пифагора:
Пусть катеты равны х, гипотенуза - с
Тогда:
с²=х²+х²=2х²
2х²=49
х²=49:2 или 49·2:4
х=√(49·2:4)=7√2):2= (3,5)√2
Катеты равны 3,5 √2 каждый.
4.2.3.
Биссектриса треугольника делит сторону на отрезки, пропорциональные прилежащим сторонам.
ВК:КС=АВ:АС
Значит, 16:АС=4:3
4 АС=48
АС=48:4=12
4.2.4 См. рисунок.
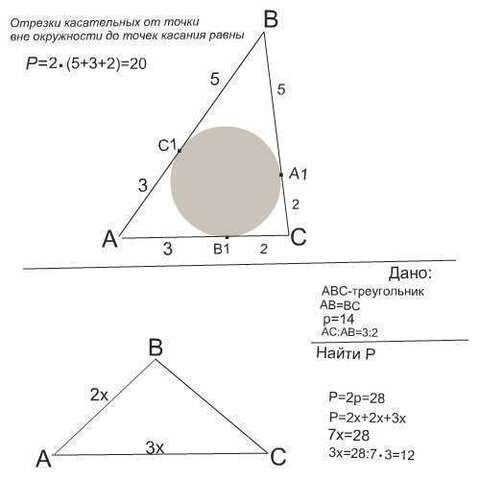
Для решения задачи нужно вспомнить, что отрезки касательных от точки вне окружности до точек касания равны между собой.
Тогда периметр окружности равен
Р=2(2+3+5)=20
------------
4.2.5.
Дано:
АВС -треугольник
АВ=ВС
полупериметр р=14
АС:АВ=3:2
Найти периметр АС
----------
Периметр Р равен 2р=14·2=28
Пусть коэффициент отношения сторон х
Тогда
боковые стороны будут по 2х, основание АС -3х
Р=2·2х+3х=7х
х=28:7=4
АС=3х=3·4=12
--------------------------
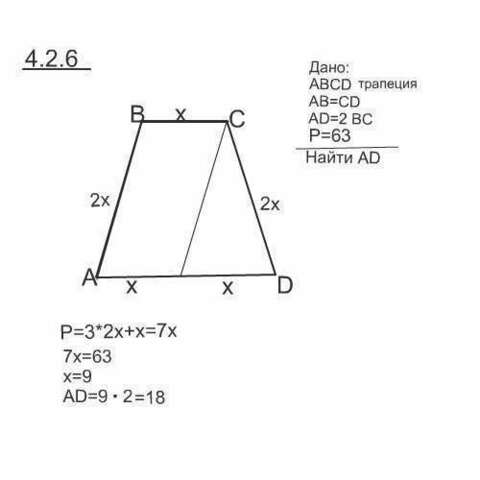
4.2.6.
Пусть меньшее основание трапеции будет х
Тогда большее основание и каждая боковая сторона 2х
Всего в периметре содержится 7х
7х=63
х=63:7=9
АD=9·2=18