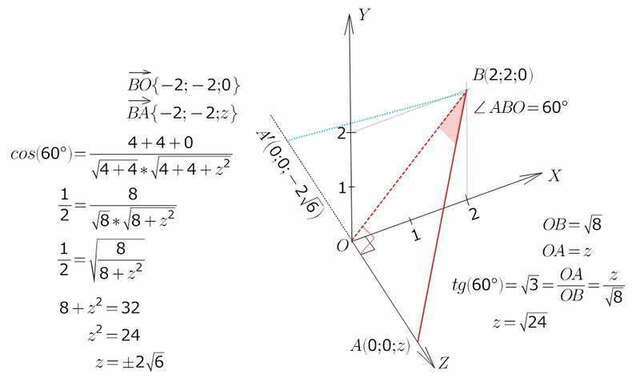
Точка В лежит в плоскости ОХУ
угол между прямой (АВ) и плоскостью --это угол между прямой и
ее проекцией на плоскость))
т.к. точка А лежит на оси OZ, проекцией прямой (АВ) будет прямая (ОВ)
т.к. не указано с какой стороны от нуля на оси OZ лежит точка А,
то возможны два варианта ее положения...
координату можно найти и из треугольника и методом координат)))