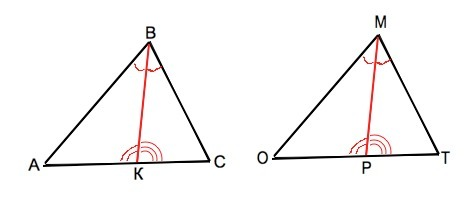
В треугольниках АВС и ОМТ биссектрисы ВК и МР равны, угол АВК=углу ОМР, угол АКВ=углу ОРМ; угол КВС=РМТ.
а) ∆ АВЕ=∆ОМР по 2-му признаку равенства треугольников.
б) ∆ КВС= ∆РМТ по 2-му признаку равенства треугольников. ⇒
∆ АВС=∆ ОМТ, так как состоят из равных частей.