В треугольнике ABC ** стороне АВ взяли точку К, а ** стороне ВС взяли точку N так, чтобы...

Question

В треугольнике ABC на стороне АВ взяли точку К, а на стороне ВС взяли точку N так, чтобы АК:КВ=СN:NB=2:1. Во сколько раз площадь АКNC больше площади треугольника KBN?

Answer 1

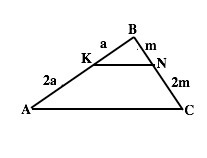
В треугольниках КВN и АВС две стороны пропорциональны, угол между ними общий, – эти треугольники подобны.

Пусть КВ=а, АК=2а, тогда

АВ=а+2а=3а

Коэффициент подобия

k=АВ:КВ=3:1

Отношение площадей подобных фигур равно квадрату коэффициента их подобия. 

S(ABC):S(KBN)=9:1

S(AKNC):S(KBN)=[S(ABC)-S(KBN)]:S(KBN)=8

Ответ: в 8 раз

---