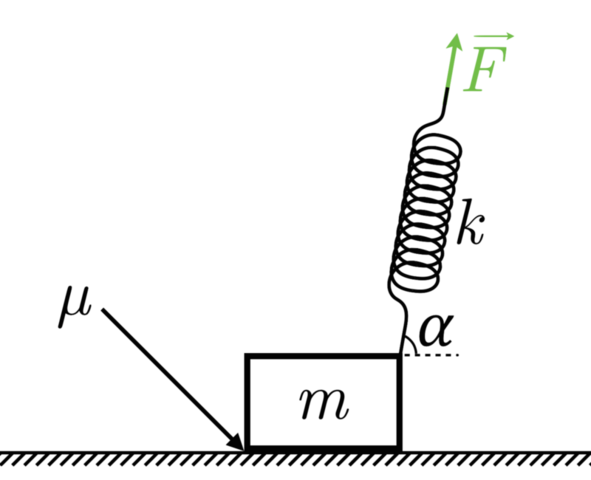
Ящик массой m=100 кг начинают тянуть с помощью пружины, имеющей жесткость k=10 kН/м, наклоненной под углом α=80∘ к горизонту. Коэффициент трения между ящиком и полом μ=0,5. Какую наименьшую работу нужно совершить внешней силой, приложенной к концу пружины, чтобы передвинуть ящик на расстояние S=1 м по прямой? Ответ выразить в Дж, округлив до целых. Считать, что ускорение свободного падения g=10 м/с2, и изначально пружина не деформирована, а при движении ящик движется равномерно.