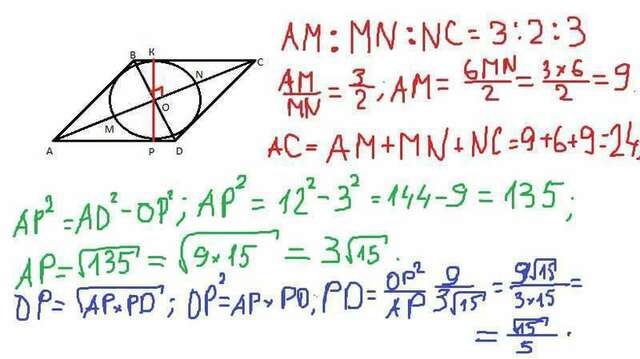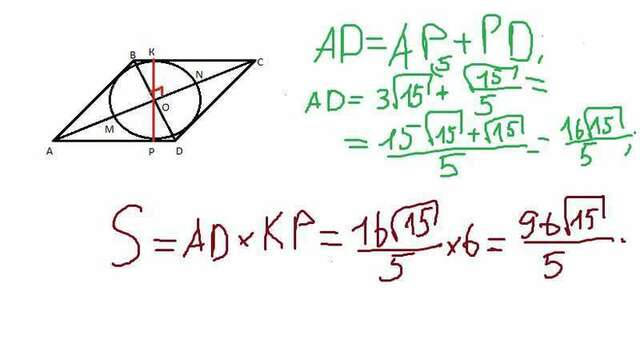Поскольку радиус равен окружности равен 3, то диаметр равен 6. Исходя из описанных в картинке действий, имеем: AC = 24, АО = 12, поскольку диагонали в точке пересечения делятся пополам, а также диагонали ромба пересекаются под прямым углом. Опустим высоту ромба КР. Теперь из прямоугольного треугольника AOP: AP^2 = AO^2 - OP^2, AP^2 = 144 - 9 - 135, АР = корень из 135 = 3 корня из 15. Поскольку ОР - высота, опущенная из прямого угла треугольника, то из подобия треугольников имеем следующее соотношение: OP^2 = AP*PD, PD = OP^2/PD = 9/3 корня из 15, PD = корень из 15 поделить на 5. AD = AP + PD = 3 корня из 15 + корень из 15 поделить на 5, AD = 16 корней из 15 поделить на 5. Площадь робма равна стороне, умноженной на опущенную к ней высоту: S = AD*KP, S = 96 корней из 15 разделить на 5.