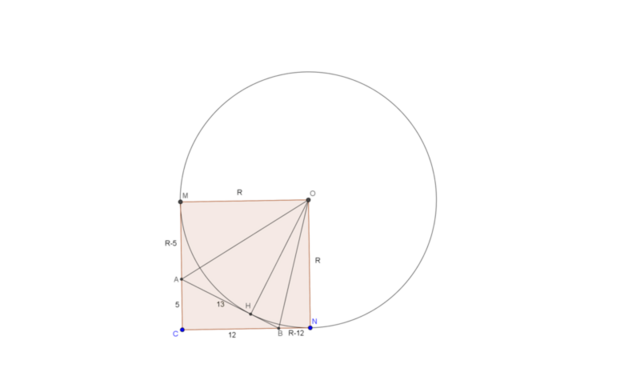
Т.к. 5²+12²=13², то треугольник ABC прямоугольный. Тогда, если С - вершина прямого угла, R - искомый радиус, а M и N - точки касания окружности с продолжениями катетов CA=5 и CB=12, то MA=R-5, NB=R-12. С другой стороны, по свойствам отрезков касательных 13=AB=MA+MB=2R-17, откуда R=15.