1.а) 
;
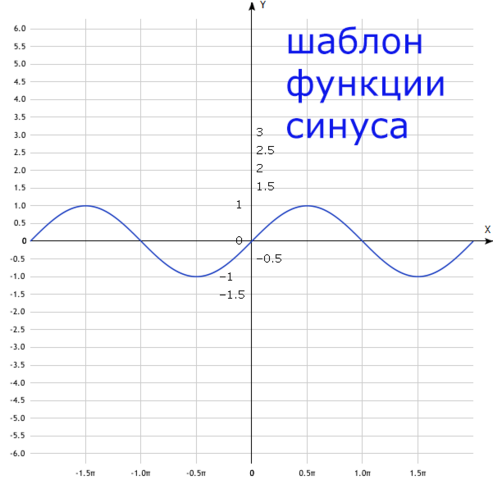
Итак, это функция синуса, её исходный шаблон представлен на первом изображении синим цветом.
Преобразуем исходное выражение функции так:
;
В таком виде можно видеть, что:
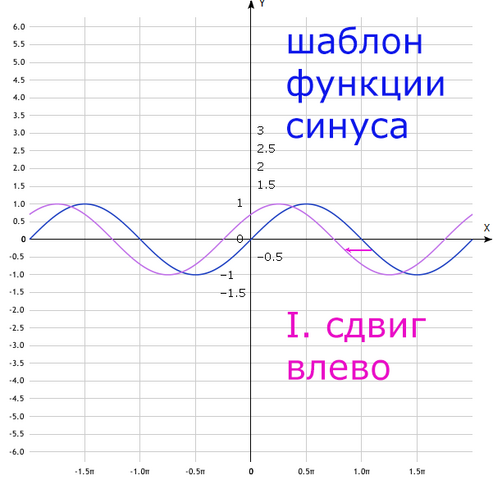
I. График смещён влево на 
, поскольку имеется знак « + » в смещении аргумента ;
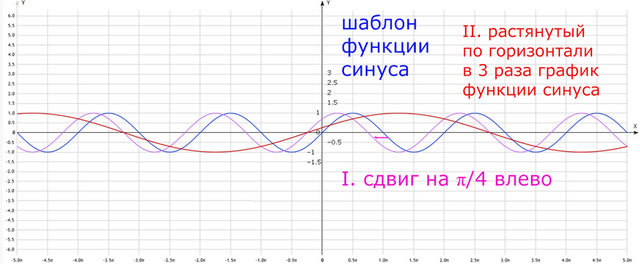
II. График растянут по горизонтали в 3 раза, поскольку при аргументе множитель 
;
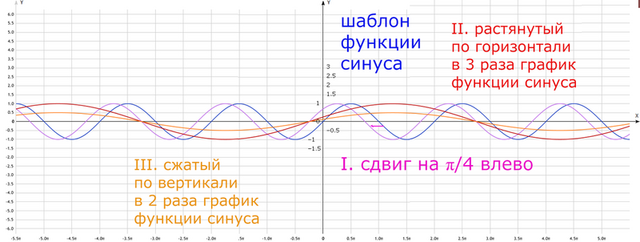
III. График сжат по вертикали в 2 раза, поскольку шаблон графика функции синуса умножен на 
;
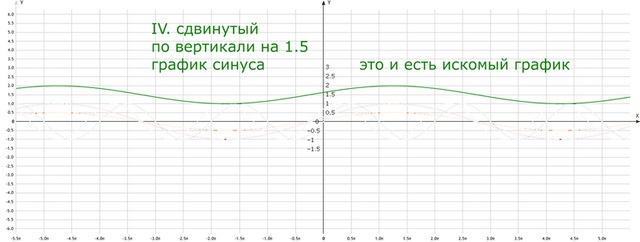
IV. График сдвинут вверх на 1.5, поскольку к деформированному шаблону графика функции синуса прибавлено 1.5 ;
I – построим сиреневым.
II – построим красным.
III – построим оранжевым.
IV – построим зелёным.
Зелёный график и есть искомый график функции 1.а)
1.2) 
;
Итак, это функция косинуса, её исходный шаблон представлен синим цветом.
Преобразуем исходное выражение функции так:
;
В таком виде можно видеть, что:
I. (сиреневый) График смещён вправо на 
, поскольку имеется знак « - » в смещении аргумента ;
II. (красный) График сжат по горизонтали в 2 раза, поскольку при аргументе множитель 
;
III. (оранжевый) График растянут по вертикали в 2 раза, поскольку шаблон графика функции косинуса умножен на ;
IV. (зелёный) График сдвинут вниз на 1, поскольку из деформированного шаблона графика функции косинуса вычтена единица ;
Здесь зелёный график – это конечный график, т.е. ответ задачи 1.2)
2.а) 
;
Итак, это функция тангенса, её исходный шаблон представлен синим цветом.
II. (красный) График растянут по горизонтали в 2 раза, поскольку при аргументе множитель ;
Здесь красный график – это конечный график, т.е. ответ задачи 2.а)
2.б) 
;
Итак, это функция котангенса, её исходный шаблон представлен синим цветом.
I. (сиреневый) График смещён вправо на , поскольку имеется знак « - » в смещении аргумента ;
IV. (зелёный) График сдвинут вверх на 1, поскольку к шаблону графика функции котангенса прибавлена единица ;
Здесь зелёный график – это конечный график, т.е. ответ задачи 2.б)
*** Остальные графики я в текст решения добавить не могу, поскольку достигнут предел по количеству изображений.
