Вычислить координаты вершины С равностороннего треугольника АВС, если даны координаты...

Question

Дан 1 ответ

Правильный ответ

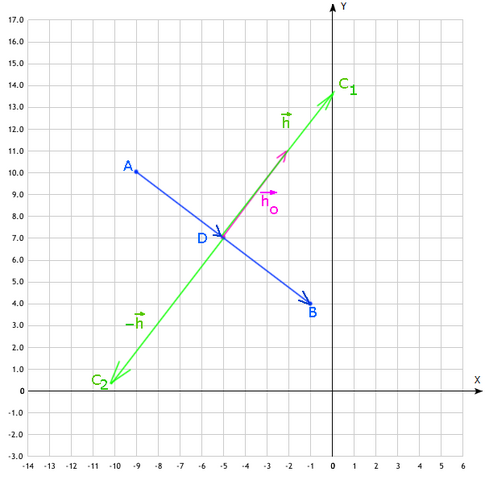
>>> идёт оформление рисунка <<< ожидайте ...<br>
Задача решается через векторы.
Построим вектор $\overline{AB} ( (-1)-(-9) , 4-10 ) = \overline{AB} ( 8 , -6 )$ ;

Середина D отрезка AB может быть найдена откладыванием половины вектора $\overline{AB}$ от точки A

$\frac{1}{2} \overline{AB} = \overline{ ( 4 , -3 ) }$ ;

Итак D( -9+4, 10-3 ) = D( -5, 7 ) ;

От точки D нужно отложить вектор высоты $\overline{h}$ в обе возможные стороны

Вектор высоты $\overline{h}$ перпендикулярен вектору основания $\overline{AB}$ , а значит его проекции накрест-пропорциональны с противоположным знаком:

(I) $\frac{x_h}{y_h} = -\frac{ y_{AB} }{ x_{AB} }$ , что непосредственно следует из скалярного произведения, поскольку для перпендикулярных векторов должно выполняться: $x_h * x_{AB} + y_h * x_{AB} = 0$ (II) ;

Таким образом вектор $\overline{h}$ пропорционален вектору $\overline{h_o} ( 3 , 4 )$ , поскольку для вектора $\overline{h_o}$ выполняется и равенство (I) и равенство (II) осталось лишь найти масштаб вектора $\overline{h}$ ;

Вектор $\overline{h_o}$ имеет длину $h_o = \sqrt{ x_{ho}^2 + y_{ho}^2 } = \sqrt{ 3^2 + 4^2 } = \sqrt{ 25 } = 5$ ;

Аналогично, AB = 10

При этом, поскольу треугольник равносторонний, то значит его высота составляет $h = \frac{ \sqrt{3} }{2}AB$ , т.к $\cos{ 60^o } = \frac{ \sqrt{3} }{2}$ ;

Значит $h = 5 \sqrt{3}$ , а стало быть $h = \sqrt{3} h_o$ ;

В итоге $\overline{h} ( 3\sqrt{3} , 4\sqrt{3} )$ .

Откладываем этот вектор в разные стороны (+\-) от точки D( -5, 7 ) и получаем:

ОТВЕТ:

$C_1 ( 3\sqrt{3} - 5 , 7 + 4\sqrt{3} )$ /// примечание: 5 " alt=" 3\sqrt{3} > 5 " align="absmiddle" class="latex-formula"> ;

$C_2 ( - 3\sqrt{3} -5 , 7 - 4\sqrt{3} )$ /// примечание: $4\sqrt{3} < 7$ .

gartenzie_zn (8.4k баллов) 13 Апр, 18