Прямоугольная трапеция соснованиями 10 см и 15 см и высотой 12 см в первый раз вращается...

Question

Дан 1 ответ

gartenzie_zn · Answer 1 · 2018-04-13T08:00:14+0000

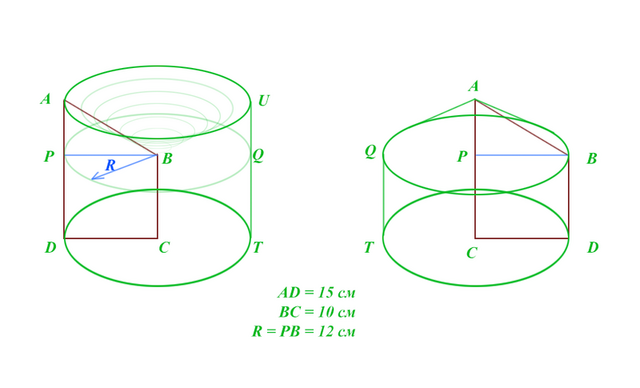
Смотрите прилагающийся к задаче рисунок.

Объём первой фигуры вращения складывается из разности объёма большого цилиндра ADTU и выбранного из него конуса ABU.

Объём конуса равен точно $\frac{1}{3}$ от объема, описанного около него малого цилиндра APQU.

Малый цилиндр APQU ровно в два раза ниже нижнего цилиндра PDTQ (так как PD = BC = 10 см, а PA = AD - BC = 5 см), а значит и объём верхнего малого цилиндра APQU в два раза меньше, чем объём нижнего цилиндра PDTQ.

В итоге мы понимаем, что объём первой фигуры равен $V_1 = V + \frac{V}{2} - \frac{1}{3} \frac{V}{2} = V ( 1 + \frac{1}{2} - \frac{1}{6} ) = 1 \frac{1}{3} V$ , где $V$ – объём нижнего цилиндра PDTQ.

Во втором случае, объём фигуры вращения складывается из суммы объёма нижнего цилиндра BDTQ (который очевидно имеет такой же объём, как и нижний цилиндр PDTQ из первого случая) и добавленного к нему конуса BAQ , который построен с такой же высотой и радиусом, как и в первом примере, а значит он тоже ровно в 6 раз меньше объёма нижнего цилиндра BDTQ.

В итоге мы понимаем, что объём второй фигуры равен $V_2 = V + \frac{1}{3} \frac{V}{2} = V ( 1 + \frac{1}{6} ) = 1 \frac{1}{6} V$ , где $V$ – объём нижнего цилиндра PDTQ.

Отношение объёмов первой и второй фигуры будет:

$\frac{ V_1 }{ V_2 } = ( 1 \frac{1}{3} V ) : ( 1 \frac{1}{6} V ) = \frac{4}{3} : \frac{7}{6} = \frac{4}{3} \cdot \frac{6}{7} = 4 \cdot \frac{2}{7} = \frac{8}{7}$ – первая фигура больше.

Найдём объём V.

Объём цилиндра PDTQ равен:

$V = BC \cdot \pi R^2 = BC \cdot \pi PB^2 = 10 \pi \cdot 12^2 = 1440 \pi$ см³ ;

Соответственно объём первой фигуры:

$V_1 = 1 \frac{1}{3} V = \frac{4}{3} \cdot 1440 \pi = 1920 \pi$ см³ $\approx 6032$ см³ $\approx 6.032$ дм³ $\approx 6.032$ л ;

И объём второй фигуры:

$V_2 = 1 \frac{1}{6} V = \frac{7}{6} \cdot 1440 \pi = 1680 \pi$ см³ $\approx 5278$ см³ $\approx 5.278$ дм³ $\approx 5.278$ л ;

О т в е т :
$V_1 = 1.92 \pi$ л (литров) ;
$V_2 = 1.68 \pi$ л (литров) ;
Отношение объёмов = 8/7. Первая фигура больше по объёму.