Итак, задание 3. Ответ будет Г). Смотри, там действует теорема о параллельности трёх прямых. MN - средняя линия ΔSBC, значит MN || BC (по свойству средней линии). А ребро BC || AD, так как в основании квадрат, а у квадрата все стороны параллельны и равны. Раз BC || AD и BC || MN, то по теореме BC || AD, а так как BC принадлежит плоскости MNPP1, где P - середина ребра AB, P1 - середина ребра CD, значит, вся плоскость параллельна плоскости SAD, которой принадлежит AD.
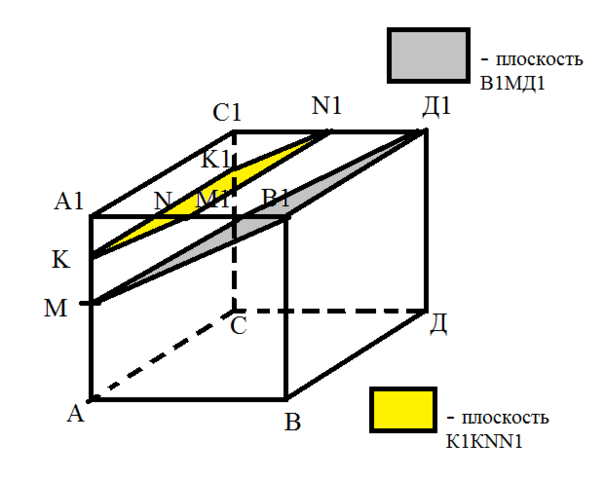
Задание 2. Я тебе нарисовала в paint. Сначала строишь плоскость B1MD1 (отмечаешь M, затем на грани CC1 середину M1, соединяешь прямую MM1. Соединяешь до плоскости B1MM1D1), затем строишь прямую KK1 (точки K и K1 - середины рёбер MA1 и C1M1 соответственно), затем прямую NN1 (точки N и N1 - середины рёбер A1B1 и C1D1 соответственно). Эти прямые у тебя автоматически параллельны прямым MM1 и B1D1. Достариваешь плоскость KNN1K1.