1)AС - катет. По теореме Пифагора: AC² = AB²-BC² = 400 - 144 = 256. AC = 16.
2) Пусть катет CA = 5x, катет CB = 12x. По теореме Пифагора AВ² = AС²+BC² =25x²+144x²=169x²
169x² = 26²
x=√(26²/169)=26/13 = 2
3)Пусть сторона квадрата равна x. Тогда по теореме Пифагора x² +x² = (4√2)²
2x² = 16*2
x² = 16
x = 4
4) Пусть неизвестная сторона прямоугольника равна x. Тогда по теореме Пифагора x² +8² = 17²
x² = 17²-8²=289 - 64 = 225
x = 15
Тогда периметр прямоугольника равен: P = (15 + 8)*2 = 46
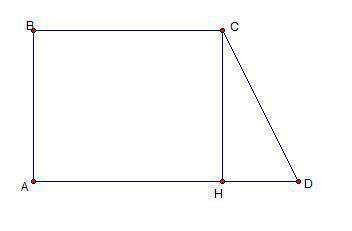
5) Из вершины С опустим высоту CH. Она будет равна стороне трапеции AC. ABCH - прямоугольник. Тогда AH = BC.
HD = AD - BC = 8,5 - 4 = 4,5.
По теореме Пифагора из треугольника HCD получим:
CD² = CH² +HD²
7,5² = CH² + 4,5²
CH² = 7,5²- 4,5² = (7,5-4,5)*(7,5+4,5) = 3*12 = 36
CH = 6
Т. к. AB = CH, то AB = 6.